However in most cases of share price movements, this assumption does not hold true. The shares are therefore observed to follow other related probability distribution functions. Hence, an indicator was made necessary to transform such prices into Gaussian normal distribution and thereby simplify identifying the trend reversals from share prices. One such highly popular indicator is the Fisher Transform indicator, which is used to transform share prices following any probability distribution function into Gaussian normal distribution and thereby helps in identifying trend reversals. The Fisher transform formula is used to convert stock prices, derivative prices, foreign exchange rates as well as technical indicators and is based on the assumption that the underlying prices would follow square wave distribution. The time series, thus transformed using the Fisher Transform formula would have very sharp turning points which prove highly simple and easier to identify bullish or bearish trends to the investors. The basic concept of Fisher Transformation was explained by J.F. Ehlers in his book “Cybernetic Analysis of Stocks and Futures” in which he had analyzed the US treasury bonds for a period of 15 years. The research on the Treasury bill rates was observed to follow a sin wave distribution rather than the normally assumed Gaussian probability distribution function. The density of price movements were observed to be highly concentrated at the left and right ends of the figure rather than around the center portion as is common with normal distribution. Further the histogram drawn using these prices showed that there was high level of occurrences in the first and last few bars, than at the middle points. This was in line with the sine distribution of the prices. As the Treasury bill rates did not follow Gaussian Distribution Function, J.F. Ehlers then moved on to derive the formula for transforming these prices into normal distribution function which was popularly known as the Fisher Transform. The formula is explained as follows: 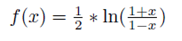 The Fisher transform could be used to transform time series data in any form of probability distribution into a Gaussian Normal Distribution function. In order to use this Fisher Transformation, the input data related to the prices of shares, Exchange Traded Funds, Foreign exchange rates or the technical indicators should first be constrained to remain within the limits of -1 to +1. Once this limitation is applied to the input data, it could then be transformed using the Fisher Transformation equation which would result in the following transformed distribution. 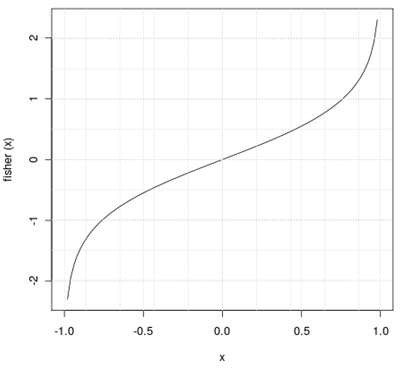 As could be observed from the above figure, when the input data of prices is near the average value ranging from -0.5 to +0.5, the transformed values are concentrated near unity i.e fisher (X) varies in the range of -1 to +1. On the other hand, when the input data is near its extreme values, the output from the Fisher Transformation is observed to be greatly magnified at the extremes. This is highly similar with the Gaussian normal distribution function, where most of the values are highly concentrated around the mean, while the extremes are observed to be concentrated at the right and left tails of the bell shaped curve. Now this information obtained from the data of Fisher Transformation could be effectively applied to extract information for determining the trading strategies for investors. As explained above, the extreme values in share prices or other input data related to prices of futures and options, foreign exchange rates or technical indicators would result in highly amplified output data in the Fisher Transformation. Thus, whenever the deep and sharp turning points are observed in the Fisher curve, investors could be clear that the rare events of peaks or bottoms have been reached by the share prices and could thereby determine their buying and selling decisions. The Fisher Transformation function could thus be effectively used to identify major turning points in the prices. This is further explained and proved by the following example: 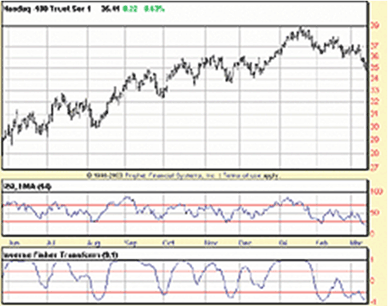 As is normally followed for calculating any technical indicator such as moving average, MACD, relative strength index or momentum, the channel or duration for the calculation of Fisher Transformation should first be determined. In this example, the 10-day channel is used for calculating the Fisher Transform. The candlestick chart for the daily price of shares for a period of six months is initially drawn. Though the candlestick chart of prices broadly indicates the price movements, the exact turning points are not clear in the chart. Following this, the Fisher Transformation of prices is then calculated and plotted to form the Fisher Chart. As you could observe, the turning points are very sharp and clear in the Fisher Transformation thus making it easier for the traders to identify. Further it could also be observed that the turning points in the Fisher Transformation appear to follow trends and patterns such that the investors could carry out profitable trades by studying them. The usefulness of the Fisher Transformation could further be ascertained by comparing it with the Moving Average Convergence and Divergence indicator curve. The turning points in MACD curve are highly smoothened that they are not much easier to identify relative to the Fisher Transformation data. The turning points in the MACD curve are round and indistinct for any investor to extract valuable information from them. On the other hand, the sharp and distinct turning points in the Fisher Transformation would mean that these are the points in the share prices or foreign exchange rates, where the investors could obtain highest rates of return. Thus the Fisher Transformation proves to be highly valuable for investors to identify those rare events or extreme values in share prices where the rate of changes are at the highest level and could thereby return the maximum to traders. comments powered by Disqus |

|
|
|
|