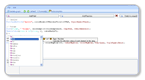
While I was working on a new trading strategy that makes extensive use of ranking and composites, I stumbled upon something that at first sight seemed to be very difficult to implement. After few minutes I found a solution but it was too complicated. Besides, the previous step was to be repeated several times and I didn't want to use the same complicated solution each time. So I discarded this idea and thought about a way to add a feature in QS trading software in order to solve the problem in one single line. This is how I come up with two more calculation methods for the composite trading indicator. These functions are named "rank!" and "percentile!" and they look pretty much like the "rank" and "percentile" functions (Trading Indicators using the Rank and Percentile functions) but there is a subtle difference. This difference lies in how "rank!" and "percentile!" treat symbols with the same values. In this case symbols will be given the same rank or percentile value, while using "rank" and "percentile", these symbols will be treated as if they have different values. Here is an example: On a particular date, we have 5 symbols with the following values: Stock1 – 25 Stock2 – 22 Stock3 – 22 Stock4 – 29 Stock5 - 21 We will now apply the "rank" and "rank!" composite functions and see how the result is different. Using the "rank" function we get the following result: Stock4 – 1 Stock1 – 2 Stock2 – 3 Stock3 – 4 Stock5 - 5 Notice how stock4 gets a rank value of one because it has the highest value and more importantly how stock2 and stock3 get different ranks even if they exactly the same value. And now let's perform the same calculation using the "rank!" function: Stock4 – 1 Stock1 – 2 Stock2 – 3 Stock3 – 3 Stock5 - 4 The last rank value is now equal to four and stock2 and stock3 have the same rank value. Concrete example using the new rank function I am sure the above example was very helpful in understanding the difference between these rank functions and this is why I am going to use another example to explain a very important usage of the "rank!" function. Let us implement the following trading strategy: Buy oversold stocks that belong to the top 3 industries based on the performance of the last month. This isn't a very simple strategy but it is I think a great example to explain our new function. The problem here concerns ranking industries. We will not get the expected results if we use the classic "rank" function, because industry rank for each stock will be different (Two stocks with the same industry will get different industry ranks). The problem can be easily solved by using "rank!" calculation method instead of "rank". Strategy Formula: os = rsi(14) < 30; // Oversold stocks indperf = comp(perf(close, 25), "avg", industry()); // Calculate the average performance per industry rankind = comp(indperf, "rank!"); // Calculate industry rank for each stock buy = os AND rankind <= 2;
|

|
|
|
|